The process of calculating a yield curve has many names in the finance industry. it can be called finding the redemption curve, constructing the term structure of interest rates, stripping and so on. In this blog post we will go through the process of constructing the yield curve for the Bloomberg SEK (vs. 6M STIBOR), also known as 348, with the help of the Python package QuantLib. When reading this tutorial consider that the main goal is to learn how to bootstrap interest rate curves with QuantLib and that Bloomberg's curve will be our answer key to make sure that everything is correct regarding dates, day count and calendar conventions. Moreover, it is assumed that the reader is familiar with instruments such as deposits and swaps - how else would you end up here?

SEK (vs. 6M STIBOR)

As shown in Figure 1, the SEK (vs. 6M STIBOR) is a swap curve based on the 6 month Stockholm Interbank Offered Rate, denoted by 6M STIBOR. The cash rate for the 6M STIBOR can be seen on the left-hand side of Figure 1, and the rates for the swaps can be seen on the right-hand side of Figure 1. The day count convention for each panel of instruments can also be observed at the bottom. The purpose of the SEK (vs. 6M STIBOR) is to forecast the interest rate for the 6M STIBOR. This means that whatever point we select on the curve is what the market will assume the 6M STIBOR will be in that amount of time.

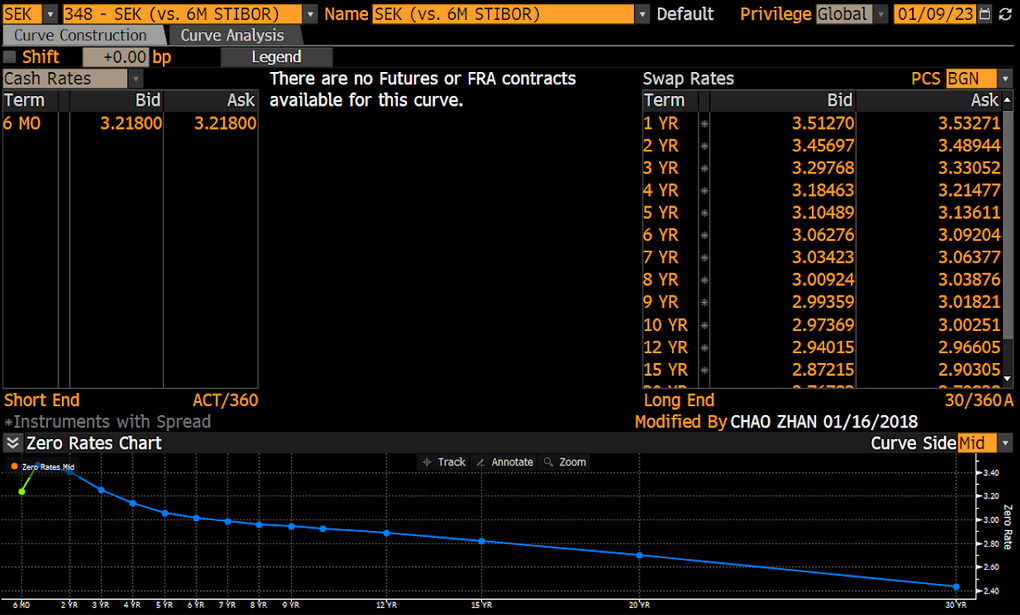
image alt text

Figure 1: Quotes for SEK (vs. 6M STIBOR) from Curve Construction in the Bloomberg Terminal.

Quantlib

We begin by setting the desired date and importing the necessary packages. The date at which the bootstrap procedure starts is determined with reference to the top right corner of Figure 2, In this case corresponding to the settlement date which often is T + 2 of the initial date in Sweden. It's important to note that this step is crucial (and may vary across trading desks) in the bootstrapping procedure, as it ensures that the maturity dates of the curve will be correct: 

import numpy as np
import quantlib as ql
from datetime import datetime, date, timedelta

# Set the valuation date
ql_date = ql.Date("2023-01-11", "%Y-%m-%d")
ql.Settings.instance().evaluationDate = ql_date

Furthermore, the main approach behind bootstrapping with QuantLib is to define all your instruments using helpers. Helpers are classes designed to define an instrument with its properties, which makes the bootstrapping procedure less cumbersome. There are helpers for each instrument such as:

  • DepositRateHelper
  • FraRateHelper
  • FuturesRateHelper

and so on, you can find the list of all helpers here. Once you have defined the instruments with helpers, you will want to store them in a list so that you can call ql.PiecewiseLinearZero(), which will find the solutions for the curve given the instruments you have defined.

Since the first instrument in curve is the 6M STIBOR, it will be the first instrument to be modeled. The 6M STIBOR is interpreted as a deposit rate, so we use the QuantLib function DepositRateHelper: 

# Create an empty array to store all the helpers as previously mentioned.
store_helpers = []

# Define all the properties of the instrument
stibor_rate = 3.21800
stibor_maturity= '6M'
stibor_calendar = ql.TARGET()
stibor_fixing_day = 0
stibor_convention = ql.ModifiedFollowing
stibor_day_counter= ql.Actual360()

# Create the DepositRateHelper
stibor_helper = ql.DepositRateHelper(ql.QuoteHandle(ql.SimpleQuote(stibor_rate/100.0)),
                    ql.Period(stibor_maturity),
                    stibor_fixing_day,
                    stibor_calendar,
                    stibor_convention,
                    False, # EOM convention
                    stibor_day_counter)
# Store the DepositRateHelper to the list of helpers
store_helpers.append(stibor_helper)

In this next step we will create the underlying index of which the floating leg will follow:

# The underlying floating rate
stibor_6m = ql.IborIndex('STIBOR6M',            # Name
                         ql.Period('6M'),       # Maturity
                         0,                     # Fixing day
                         ql.SEKCurrency(),      # Currency
                         ql.TARGET(),           # Calendar
                         ql.ModifiedFollowing,  # Calendar convention
                         ql.Actual360())        # Day count

Moreover, the swap rates in Figure 1 are given as ask and bid. The bootstrap procedure is based on the mid price, which is based on the average of the bid and ask: 

# Calculate the mid quotes
bid_list= [3.51270, 3.45697, 3.29768, 3.18463,
 3.10489, 3.06276, 3.03423, 3.00924,
 2.99359, 2.97369, 2.94015, 2.87215,
 2.76782, 2.54788]
ask_list = [3.53271, 3.48944, 3.33052, 3.21477,
 3.13611, 3.09204, 3.06377, 3.03876,
 3.01821, 3.00251, 2.96605, 2.90305,
 2.79838, 2.57832]
mid = [(bid + ask)/2 for bid, ask in zip(bid_list,ask_list)]

Then continuing with SwapRateHelper: 

fixedFrequency = ql.Annual                           # Frequency of the fixed leg
fixedConvention = ql.ModifiedFollowing               # Fixed leg convention
fixedDayCount = ql.Thirty360(ql.Thirty360.BondBasis) # Daycount convention of the fixed leg
calendar = ql.TARGET()

tenor =['1Y', '2Y', '3Y', '4Y',
        '5Y', '6Y', '7Y', '8Y',
        '9Y', '10Y', '12Y','15Y',
        '20Y', '30Y']
iborIndex = index
for r,m in zip(mid, tenor):
    rate = ql.QuoteHandle(ql.SimpleQuote(r/100.0))
    tenor = ql.Period(m)
    swap_helper = swap_helper = ql.SwapRateHelper(
    rate, tenor, calendar, fixedFrequency, fixedConvention, fixedDayCount, stibor_6m
    )

    # Append each swap to our store_helpers
    store_helpers.append(swap_helper)

Now that all instruments are defined we can execute the bootstrapping algorithm by using the following: 

curve = ql.PiecewiseLinearZero(0, ql.TARGET(), helpers, ql.Actual365Fixed())

Note that you also have the option to change the calendar and the day count for the bootstrap. You can modify these parameters based on your desired outcome.

Result

The zero rates obtained from Bloomberg are displayed in Figure 2. MEanwhile, the resulting curve generated from QuantLib is shown in Figure 3. To facilitate the comparison of the curves, a table is created to calculate the difference between the results, as presented in Table 1. It is important to note that the basis point difference can be disregarded, as the result from Bloomberg is rounded. Therefore, any extra digits in the basis point difference are solely from the QuantLib approximation. If we were to round them up, they would result in zeros.

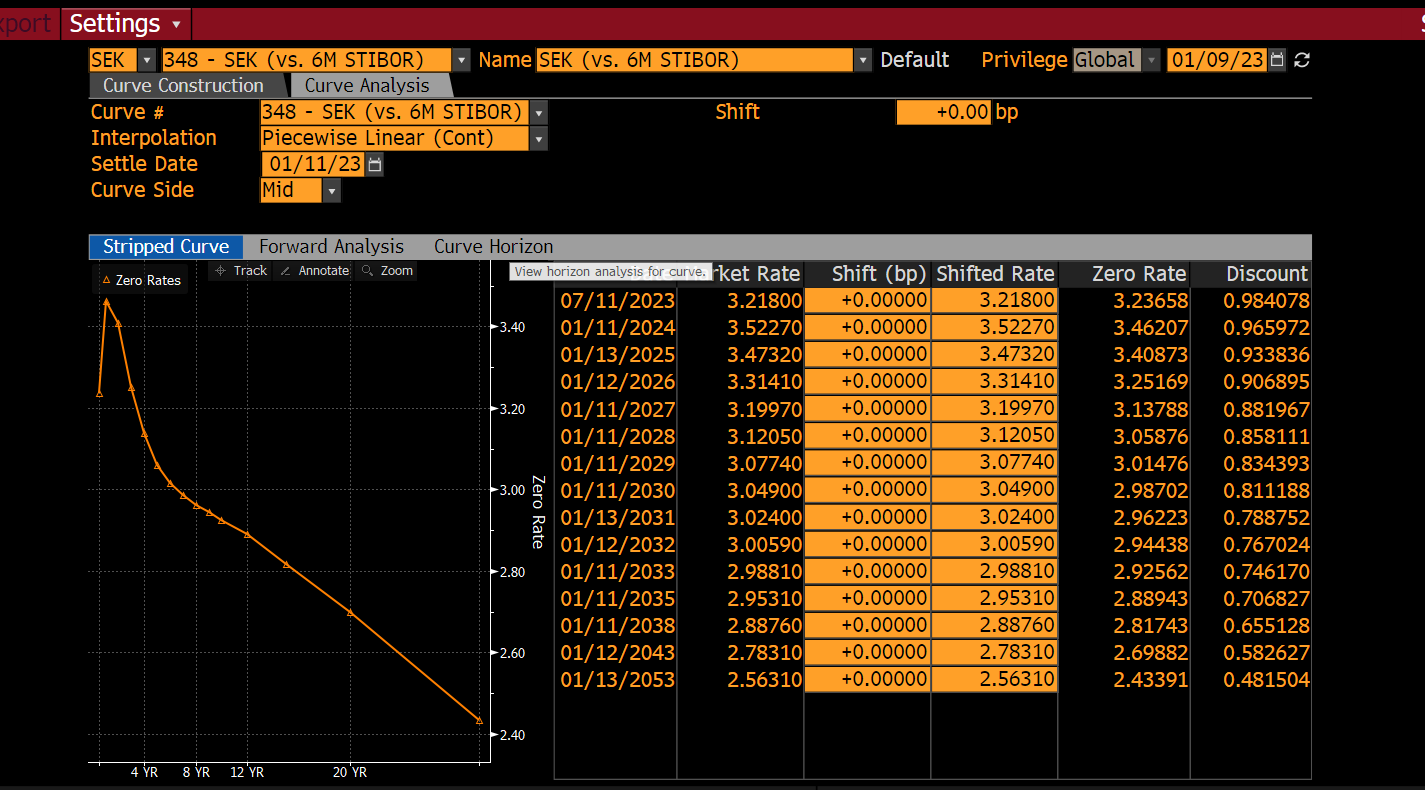
image alt text

Figure 2: The Bloomberg curve SEK (vs. 6M STIBOR) from Curve Construction in the Bloomberg Terminal.

image alt text

Figure 3: The resulting curve from QuantLib using quotes from Bloomberg.

  Date Quotes QuantLib Zero Rates Bloomberg Zero Rates Basis Point Difference
1 2023-07-13 3.218 3.23658 3.23658 -0.015275
2 2024-01-11 3.52271 3.46208 3.46207 -0.0746395
3 2025-01-13 3.47321 3.40873 3.40873 -0.04655
4 2026-01-12 3.3141 3.25169 3.25169 -0.0397416
5 2027-01-11 3.1997 3.13788 3.13788 0.038115
6 2028-01-11 3.1205 3.05876 3.05876 -0.0230695
7 2029-01-11 3.0774 3.01476 3.01476 0.0163274
8 2030-01-11 3.049 2.98702 2.98702 -0.00937578
9 2031-01-13 3.024 2.96223 2.96223 -0.0348135
10 2032-01-12 3.0059 2.94438 2.94438 -0.0386432
11 2033-01-11 2.9881 2.92562 2.92562 0.0279722
12 2035-01-11 2.9531 2.88943 2.88943 -0.0104289
13 2038-01-11 2.8876 2.81743 2.81743 -0.0475918
14 2043-01-12 2.7831 2.69882 2.69882 -0.0153047
15 2053-01-13 2.5631 2.43391 2.43391 -0.0218202

Table 1: QuantLib and Bloomberg zero rates with their corresponding underlying quotes.

Conclusion

In this blog post we have managed to recreate the SEK (vs. 6M STIBOR) from curve construction from the Bloomberg Terminal using QuantLib. If you are interested in the full Python code you can find here.

References

  • Luigi Ballabio, Implementing QuantLib: Quantitative finance in C++: an inside look at the architecture of the QuantLib library, Autopubblicato
  • Bloomberg L.P., SEK (vs. 6M STIBOR)
<
Blog Archive
Archive of all previous blog posts
>
Next Post
Creating Curves in RatesLib Versus QuantLib